Difference between revisions of "Accurately Calculating Sugar Additions for Carbonation"
(→dried malt extract) |
|||
| (27 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Carbonation calculation spreadsheet [http://braukaiser.com/documents/Kaiser_carbonation_calculator_US.xls preloaded with US unis] or [http://braukaiser.com/documents/Kaiser_carbonation_calculator_metric.xls preloaded with metric units] for quick access. But you may want to read this article to understand how it works. | |
| − | + | Accurately calculating the carbonation is a great exercise for working with apparent and true (or real) attenuations as well as working with the extract % or Plato scale. The latter is not essential, but makes the calculations more intuitive. | |
| − | The amount of CO<sub>2</sub> already in the beer | + | The final carbonation of bottle conditioned beer depends on the CO<sub>2</sub> present in the beer at bottling time and the CO<sub>2</sub> that will be generated during bottle conditioning. |
| + | |||
| + | The amount of CO<sub>2</sub> already in the beer can be determined based on the CO<sub>2</sub> head-space pressure and the temperature of the beer. It can be determined by using [[Carbonation Tables]]. These tables show the equilibrium of CO<sub>2</sub> content that exists for a given CO<sub>2</sub> pressure and beer temperature. | ||
The amount of CO>sub>2</sub> created by bottle conditioning is based on the amount of sugar that is fermented. Each gram of fermentable extract is fermented into equal parts (by weight) of alcohol and CO<sub>2</sub> (this is not exactly true, but close enough for this calculation). | The amount of CO>sub>2</sub> created by bottle conditioning is based on the amount of sugar that is fermented. Each gram of fermentable extract is fermented into equal parts (by weight) of alcohol and CO<sub>2</sub> (this is not exactly true, but close enough for this calculation). | ||
| − | = | + | =Converting Units= |
| + | |||
| + | Since this article is written using metric units, the following formulas can be used to convert from/to units commonly used by American home brewers: | ||
| + | |||
| + | '''<tt>1 g = 0.035 oz</tt>''' | ||
| + | |||
| + | '''<tt>1 l = 1.06 qt</tt>''' | ||
| + | |||
| + | '''<tt>1 g/l CO<sub>2</sub> = 0.5 volumes CO<sub>2</sub></tt>''' | ||
| + | |||
| + | '''<tt>1 Plato = -463.37 + (668.72 × SG) - (205.35 × SG<sup>2</sup>)</tt>''' [ENSMINGER], or '''<tt>1 Plato = (SG - 1) * 1000 / 4</tt>''' for a quick conversion | ||
| + | |||
| + | =Corn Sugar= | ||
| − | The easiest way to add fermentable extract to beer is through the addition of pure sugar. This can be dextrose (corn sugar) or | + | The easiest way to add fermentable extract to beer is through the addition of pure sugar. This can be dextrose (corn sugar) or sucrose (table sugar). Most corn sugar is actually glucose monohydrate. This means that each glucose molecule bound with a water molecule which adds to its weight but not to the potential of CO<sub>2</sub> that can be produced [McGill]. Glucose monohydrate contains 9% water by weight, which means that only 91% of its weight can be considered for the CO<sub>2</sub> calculation. Glucose monohydrate is the corn sugar that doesn't clump when not stored in a sealed container. |
The formula for calculating the carbonation when priming with corn sugar is: | The formula for calculating the carbonation when priming with corn sugar is: | ||
| Line 22: | Line 36: | ||
=table sugar= | =table sugar= | ||
| − | Table sugar, | + | Table sugar, sucrose, does not contain any water and yeast will convert half of its weight to CO<sub>2</sub> |
'''C<sub>beer</sub> = C<sub>flat-beer</sub> + 0.5 * m<sub>table-sugar</sub> / V<sub>beer</sub>''' | '''C<sub>beer</sub> = C<sub>flat-beer</sub> + 0.5 * m<sub>table-sugar</sub> / V<sub>beer</sub>''' | ||
| − | * m<sub>table-sugar</sub> - the weight of the table sugar ( | + | * m<sub>table-sugar</sub> - the weight of the table sugar (sucrose) (g) |
| − | = | + | =Dried Malt Extract= |
| − | When using malt extract for priming, its fermentability needs to be taken into account. A typical | + | When using malt extract for priming, its fermentability needs to be taken into account. A typical apparent fermentability (limit of attenuation) of malt extract is 80%. (a 12 Plato wort will finish at 2.4 Plato / 1.048 OG - 1.010 FG). But in order to calculate the amount of fermentable sugars in DME, the true attenuation needs to be calculated. To convert between apparent and true attenuation, the following formula can be used (see [[Understanding Attenuation]]) |
'''<tt>A<sub>true</sub> = A<sub>apparent</sub> * 0.82</tt>''' | '''<tt>A<sub>true</sub> = A<sub>apparent</sub> * 0.82</tt>''' | ||
| Line 48: | Line 62: | ||
=Speise= | =Speise= | ||
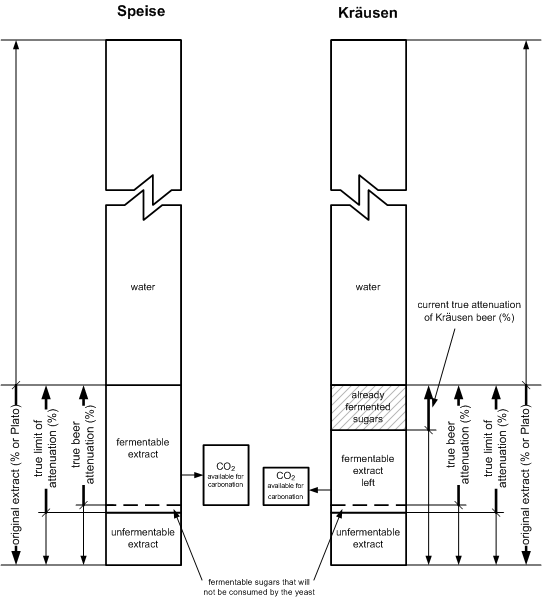
| + | [[Image:Carbonation_from_Speise.gif|frame|Figure 1 - the fermentable extract in Speise and Kraeusen]] | ||
| + | |||
| + | The carbonation calculation with Speise is similar to the calculation for malt extract with the difference that the fermentability is known and that the volume of the beer, that is going to be bottled, is increased by the Speise volume. Though water is used for the priming with sugar and DME its contribution to the beer volume are small and have been neglected. But when using Speise or Kraeusen, the amount of volume that is added can be significant. | ||
| + | |||
| + | First, the apparent attenuation of the Speise needs to be determined. If using wort from a previously brewed batch, generally the same batch that needs to be carbonated, the original extract and final extract are known. When boiling the Speise to sanitize it before bottling, make sure you boil with a lid on to minimize evaporation loss (which changes its original extract) or compensate for it by adding water or adjusting the original extract that is used in the equations. You could weigh the boiling vessel with the Speise before and after the boil and add sanitary water to compensate for evaporation. | ||
| + | |||
| + | '''<tt>AA<sub>Speise</sub> = 100 - 100 * FE<sub>Speise</sub> / OE<sub>Speise</sub></tt>''' | ||
| + | |||
| + | * AA<sub>Speise</sub> - apparent attenuation of the Speise wort | ||
| + | * OE<sub>Speise</sub> - original extract of the Speise wort | ||
| + | * FE<sub>Speise</sub> - the expected final extract of the Speise wort. Take the final gravity reading of the beer for this. | ||
| + | |||
| + | From the apparent attenuation we can calculate the real attenuation with | ||
| + | |||
| + | '''<tt>RA<sub>Speise</sub> = 0.82 * AA<sub>Speise</sub></tt>''' | ||
| + | |||
| + | The real attenuation tells how what percentage of the original extract of the Speise is actually fermentable and will contribute to the carbonation of the beer. With the Plato or percent extract scale, the amount of extract (sugars, proteins, dextrines ... everything that is dissolved in the water) in a given wort can easily be calculated with | ||
| + | |||
| + | '''<tt>m<sub>extract</sub> = V<sub>Speise</sub> * sg * OE/100</tt>''' | ||
| + | |||
| + | * m<sub>extract</sub> - extract weight (g) | ||
| + | * V<sub>Speise</sub> - volume of the wort (ml) | ||
| + | * sg - specific gravity of the wort. This can be ommitted for lower gravity beers as it will be close enough to 1. sg ~ 1 + OE/250 | ||
| + | * OE - original extract in % or Plato | ||
| + | |||
| + | The amount of fermentable extract can be determined by scaling the extract weight with the true attenuation (RA) | ||
| + | |||
| + | '''<tt>m<sub>fermentable-extract</sub> = m<sub>extract</sub> * RA</tt>''' | ||
| + | |||
| + | * m<sub>fermentable-extract</sub> - the weight of the fermentable extract | ||
| + | |||
| + | At this point the known carbonation equations can be used with the difference that the volume of the final beer is now the Volume of | ||
| + | the beer before bottling plus the Speise volume. Note that this equation does consider the Speise saturated with CO<sub>2</sub> which is not true, but omitting this fact makes it a little easier and doesn't throw off the result by much since the carbonation contributed by that is fairly small. | ||
| + | |||
| + | '''<tt>C<sub>beer</sub> = C<sub>flat-beer</sub> + 0.5 * m<sub>fermentable-extract</sub> / (V<sub>flat-beer</sub> + V<sub>Speise</sub>)</tt>''' | ||
| + | |||
| + | * C<sub>beer</sub> - the final carbonation of the beer (g/l) | ||
| + | * C<sub>flat-beer</sub> - the CO<sub>2</sub> content of the beer before bottling (g/l) | ||
| + | * V<sub>flat-beer</sub> - beer volume before bottling (l) | ||
| + | |||
| + | =Kraeusen Beer= | ||
| + | |||
| + | The calculations for Kraeusen beer are similar to the ones necessary for Speise with the exception that the current attenuation of | ||
| + | the Kraeusen beer should be taken into account. This can easily be done by taking a gravity reading shortly before it is used for | ||
| + | priming. From that we can calculate the apparent attenuation and real attenuation | ||
| + | |||
| + | '''<tt>RA<sub>current-Kraeusen</sub> = 0.82 * (1 - OE<sub>Kraeusen</sub> / AE<sub>Kraeusen</sub>)</tt>''' | ||
| + | |||
| + | '''<tt>RA<sub>final-Kraeusen</sub> = 0.82 * (1 - OE<sub>Kraeusen</sub> / FE<sub>Kraeusen</sub>)</tt>''' | ||
| + | |||
| + | * RA<sub>current-Kraeusen</sub> - the current true attenuation of the Kraeusen beer (%) | ||
| + | * OE<sub>Kraeusen</sub> - the original extract of the Kraeusen wort (Plato) | ||
| + | * AE<sub>Kraeusen</sub> - the current measured extract of the Kraeusen beer (Plato) | ||
| + | * FE<sub>Kraeusen</sub> - the expected final extract of the Kraeusen wort (Plato). Take the final gravity reading of the beer for this. | ||
| + | |||
| + | The amount of fermentables left in the Kraeusen is based on the difference between the current true attenuation | ||
| + | (RA<sub>current-Kraeusen</sub>) and the exptected true final attenuation RA<sub>final-Kraeusen</sub> | ||
| + | |||
| + | '''<tt>m<sub>fermentable-kraeusen</sub> = V<sub>Kraeusen</sub> * SG * OE/100 * (RA<sub>final-Kraeusen</sub> - | ||
| + | RA<sub>current-Kraeusen</sub>)</tt>''' | ||
| + | |||
| + | * m<sub>fermentable-kraeusen</sub> - amount of fermentables left in Kraeusen beer (g) | ||
| + | * V<sub>Kraeusen</sub> - Kraeusen beer volume (ml) | ||
| + | * SG - Specific gravity of the Kraeusen. Take either the starting gravity or the current gravity of the Kraeusen. If the current | ||
| + | attenuation is low and/or the starting gravity was low to begin with, this factor won't make much of a difference and I actually | ||
| + | omit it alltogether. | ||
| + | |||
| + | Once we have the amount of fermentable extract left in the Kraeusen, we can calculate its carbonation contribution. | ||
| + | |||
| + | '''<tt>C<sub>beer</sub> = C<sub>flat-beer</sub> + 0.5 * m<sub>fermentable-Kraeusen</sub> / (V<sub>flat-beer</sub> + V<sub>Kraeusen</sub>)</tt>''' | ||
| + | |||
| + | =Remaining or Residual Extract= | ||
| + | |||
| + | The last form of priming, that should be discussed here, is carbonating with remaining (fermentable) extract. For that, a fast ferment test must have been done to determine the limit of attenuation of the beer that is going to be bottled since the beer will be bottled before it is actually done fermenting. In its purest form it means that the bottling time is going to be determined by the rate of fermentation of the beer. While this is rather unpractical, what if the desired bottling extract level is reached while you are at work, taking the remaining fermentable extract into account when calculating carbonation allows the brewer to bottle even before a batch is completely done fermenting. Such a scenario can easily happen when a beer is fermented rather cold and the primary or secondary fermentation is taking its time. Once the extract level is below a level that causes over-carbonation, you are ok to bottle the beer. The method of bottling with remaining extract is also useful for quick bottling of samples from a primary. | ||
| + | |||
| + | Using the previously described formulas, you can calculate the amount of fermentable extract that is lef in a beer if you know the gravity or extract content of the fast ferment test (measured with a hydrometer) and the current gravity or extract content of the beer. | ||
| + | Note that your yeast may not ferment all the way to the wort's attenuation limit. Depending on the strain, its health and other factors, the final attenuation might be a little lower than the limit of attenuation. If you don't know this number, just assume that this difference is 0. You can check this later by taking an final extract measurement of the bottled beer after it has been conditioned. | ||
| + | |||
| + | Here I want to demonstrate a different approach of calculating the carbonation. This approach works entirely with true extract percentages and their difference. | ||
| + | |||
| + | '''<tt>delta RE = 0.82 * (AE<sub>current beer</sub>) - AE<sub>expected final</sub>)</tt>''' | ||
| + | |||
| + | * RE - The real extract difference between the current beer and the finished beer (% w/w or Plato). | ||
| + | * AE<sub>current beer</sub> - the current measured extract of the beer (% w/w or Plato) | ||
| + | * AE<sub>expected final</sub>) - The expected final extract is taken from the fast ferment test (% w/w or Plato). | ||
| + | delta RE represents the weight percentage of residual fermentable sugar that is still present in the beer. From this it is easy to calculate the amount of carbonation that can be expected. Each % w/w (or Plato) of fermentable sugar will yield 0.5 % w/w CO<sub>2</sub> and 0.5 % w/w alcohol. 1 g/l CO<sub>2</sub> is also 0.1 % w/w CO<sub>2</sub> which is used to calculate the expected carbonation from the real extract difference: | ||
| + | '''<tt>c<sub>residual extract</sub> = 5 * delta RE</tt>''' | ||
| + | |||
| + | * c<sub>residual extract</sub> - the carbonation from residual fermentable extract in g/l | ||
| + | Based on these calculations the following guidelines can be derived: | ||
| + | * Each degree Plato yields 4.1 g/l or 2 volumes CO<sub>2</sub> | ||
| + | * Each gravity point yields 1 g/l or 0.51 volumes CO<sub2</sub> | ||
| + | = Final Remarks = | ||
| + | While the number of formulas is daunting, they give the brewer more flexibility over the priming process especially since they can be combined. While priming with Kraeusen I may want to add sugar because the Kraeusen volume is to small or to far attenuated. Oftentimes I also have to account for remaining fermentable extract in the beer because I crashed the yeast to early or the fermentation was just dragging on. Because of that I created a spreadsheet (preloaded with [http://braukaiser.com/documents/Kaiser_carbonation_calculator_US.xls US units]|[http://braukaiser.com/documents/Kaiser_carbonation_calculator_metric.xls metric units]) into which I simply enter all the data that I have and play with the volumes and amounts of sugar until the desired carbonation is reached. | ||
=sources= | =sources= | ||
| − | * [ | + | * [McGill] - Robert McGill, Priming With Sugar [http://www.byo.com/feature/1542.html BYO article] |
| + | * [ENSMINGER] - Peter A. Ensminger, Beer Data on HBD [http://hbd.org/ensmingr/ HBD article] | ||
Latest revision as of 00:21, 24 September 2012
Carbonation calculation spreadsheet preloaded with US unis or preloaded with metric units for quick access. But you may want to read this article to understand how it works.
Accurately calculating the carbonation is a great exercise for working with apparent and true (or real) attenuations as well as working with the extract % or Plato scale. The latter is not essential, but makes the calculations more intuitive.
The final carbonation of bottle conditioned beer depends on the CO2 present in the beer at bottling time and the CO2 that will be generated during bottle conditioning.
The amount of CO2 already in the beer can be determined based on the CO2 head-space pressure and the temperature of the beer. It can be determined by using Carbonation Tables. These tables show the equilibrium of CO2 content that exists for a given CO2 pressure and beer temperature.
The amount of CO>sub>2</sub> created by bottle conditioning is based on the amount of sugar that is fermented. Each gram of fermentable extract is fermented into equal parts (by weight) of alcohol and CO2 (this is not exactly true, but close enough for this calculation).
Contents
Converting Units
Since this article is written using metric units, the following formulas can be used to convert from/to units commonly used by American home brewers:
1 g = 0.035 oz
1 l = 1.06 qt
1 g/l CO2 = 0.5 volumes CO2
1 Plato = -463.37 + (668.72 × SG) - (205.35 × SG2) [ENSMINGER], or 1 Plato = (SG - 1) * 1000 / 4 for a quick conversion
Corn Sugar
The easiest way to add fermentable extract to beer is through the addition of pure sugar. This can be dextrose (corn sugar) or sucrose (table sugar). Most corn sugar is actually glucose monohydrate. This means that each glucose molecule bound with a water molecule which adds to its weight but not to the potential of CO2 that can be produced [McGill]. Glucose monohydrate contains 9% water by weight, which means that only 91% of its weight can be considered for the CO2 calculation. Glucose monohydrate is the corn sugar that doesn't clump when not stored in a sealed container.
The formula for calculating the carbonation when priming with corn sugar is:
Cbeer = Cflat-beer + 0.5 * 0.91 * mcorn-sugar / Vbeer
- Cbeer - the final carbonation of the beer (g/l)
- Cflat-beer - the CO2 content of the beer before bottling (g/l)
- mcorn-sugar - the weight of the corn sugar (glucose monohydrate) (g)
- Vbeer - beer volume (l)
table sugar
Table sugar, sucrose, does not contain any water and yeast will convert half of its weight to CO2
Cbeer = Cflat-beer + 0.5 * mtable-sugar / Vbeer
- mtable-sugar - the weight of the table sugar (sucrose) (g)
Dried Malt Extract
When using malt extract for priming, its fermentability needs to be taken into account. A typical apparent fermentability (limit of attenuation) of malt extract is 80%. (a 12 Plato wort will finish at 2.4 Plato / 1.048 OG - 1.010 FG). But in order to calculate the amount of fermentable sugars in DME, the true attenuation needs to be calculated. To convert between apparent and true attenuation, the following formula can be used (see Understanding Attenuation)
Atrue = Aapparent * 0.82
- Atrue - true attenuation
- Aapparent - apparent attenuation
With that the carbonation that can be achieved with dried malt extract is
Cbeer = Cflat-beer + 0.5 * 0.82 * 0.80 * mDME / Vbeer
- Cbeer - the final carbonation of the beer (g/l)
- Cflat-beer - the CO2 content of the beer before bottling (g/l)
- mDME - the weight of the dried malt extract (DME) (g)
- Vbeer - beer volume (l)
Speise
The carbonation calculation with Speise is similar to the calculation for malt extract with the difference that the fermentability is known and that the volume of the beer, that is going to be bottled, is increased by the Speise volume. Though water is used for the priming with sugar and DME its contribution to the beer volume are small and have been neglected. But when using Speise or Kraeusen, the amount of volume that is added can be significant.
First, the apparent attenuation of the Speise needs to be determined. If using wort from a previously brewed batch, generally the same batch that needs to be carbonated, the original extract and final extract are known. When boiling the Speise to sanitize it before bottling, make sure you boil with a lid on to minimize evaporation loss (which changes its original extract) or compensate for it by adding water or adjusting the original extract that is used in the equations. You could weigh the boiling vessel with the Speise before and after the boil and add sanitary water to compensate for evaporation.
AASpeise = 100 - 100 * FESpeise / OESpeise
- AASpeise - apparent attenuation of the Speise wort
- OESpeise - original extract of the Speise wort
- FESpeise - the expected final extract of the Speise wort. Take the final gravity reading of the beer for this.
From the apparent attenuation we can calculate the real attenuation with
RASpeise = 0.82 * AASpeise
The real attenuation tells how what percentage of the original extract of the Speise is actually fermentable and will contribute to the carbonation of the beer. With the Plato or percent extract scale, the amount of extract (sugars, proteins, dextrines ... everything that is dissolved in the water) in a given wort can easily be calculated with
mextract = VSpeise * sg * OE/100
- mextract - extract weight (g)
- VSpeise - volume of the wort (ml)
- sg - specific gravity of the wort. This can be ommitted for lower gravity beers as it will be close enough to 1. sg ~ 1 + OE/250
- OE - original extract in % or Plato
The amount of fermentable extract can be determined by scaling the extract weight with the true attenuation (RA)
mfermentable-extract = mextract * RA
- mfermentable-extract - the weight of the fermentable extract
At this point the known carbonation equations can be used with the difference that the volume of the final beer is now the Volume of the beer before bottling plus the Speise volume. Note that this equation does consider the Speise saturated with CO2 which is not true, but omitting this fact makes it a little easier and doesn't throw off the result by much since the carbonation contributed by that is fairly small.
Cbeer = Cflat-beer + 0.5 * mfermentable-extract / (Vflat-beer + VSpeise)
- Cbeer - the final carbonation of the beer (g/l)
- Cflat-beer - the CO2 content of the beer before bottling (g/l)
- Vflat-beer - beer volume before bottling (l)
Kraeusen Beer
The calculations for Kraeusen beer are similar to the ones necessary for Speise with the exception that the current attenuation of the Kraeusen beer should be taken into account. This can easily be done by taking a gravity reading shortly before it is used for priming. From that we can calculate the apparent attenuation and real attenuation
RAcurrent-Kraeusen = 0.82 * (1 - OEKraeusen / AEKraeusen)
RAfinal-Kraeusen = 0.82 * (1 - OEKraeusen / FEKraeusen)
- RAcurrent-Kraeusen - the current true attenuation of the Kraeusen beer (%)
- OEKraeusen - the original extract of the Kraeusen wort (Plato)
- AEKraeusen - the current measured extract of the Kraeusen beer (Plato)
- FEKraeusen - the expected final extract of the Kraeusen wort (Plato). Take the final gravity reading of the beer for this.
The amount of fermentables left in the Kraeusen is based on the difference between the current true attenuation (RAcurrent-Kraeusen) and the exptected true final attenuation RAfinal-Kraeusen
mfermentable-kraeusen = VKraeusen * SG * OE/100 * (RAfinal-Kraeusen - RAcurrent-Kraeusen)
- mfermentable-kraeusen - amount of fermentables left in Kraeusen beer (g)
- VKraeusen - Kraeusen beer volume (ml)
- SG - Specific gravity of the Kraeusen. Take either the starting gravity or the current gravity of the Kraeusen. If the current
attenuation is low and/or the starting gravity was low to begin with, this factor won't make much of a difference and I actually omit it alltogether.
Once we have the amount of fermentable extract left in the Kraeusen, we can calculate its carbonation contribution.
Cbeer = Cflat-beer + 0.5 * mfermentable-Kraeusen / (Vflat-beer + VKraeusen)
Remaining or Residual Extract
The last form of priming, that should be discussed here, is carbonating with remaining (fermentable) extract. For that, a fast ferment test must have been done to determine the limit of attenuation of the beer that is going to be bottled since the beer will be bottled before it is actually done fermenting. In its purest form it means that the bottling time is going to be determined by the rate of fermentation of the beer. While this is rather unpractical, what if the desired bottling extract level is reached while you are at work, taking the remaining fermentable extract into account when calculating carbonation allows the brewer to bottle even before a batch is completely done fermenting. Such a scenario can easily happen when a beer is fermented rather cold and the primary or secondary fermentation is taking its time. Once the extract level is below a level that causes over-carbonation, you are ok to bottle the beer. The method of bottling with remaining extract is also useful for quick bottling of samples from a primary.
Using the previously described formulas, you can calculate the amount of fermentable extract that is lef in a beer if you know the gravity or extract content of the fast ferment test (measured with a hydrometer) and the current gravity or extract content of the beer. Note that your yeast may not ferment all the way to the wort's attenuation limit. Depending on the strain, its health and other factors, the final attenuation might be a little lower than the limit of attenuation. If you don't know this number, just assume that this difference is 0. You can check this later by taking an final extract measurement of the bottled beer after it has been conditioned.
Here I want to demonstrate a different approach of calculating the carbonation. This approach works entirely with true extract percentages and their difference.
delta RE = 0.82 * (AEcurrent beer) - AEexpected final)
- RE - The real extract difference between the current beer and the finished beer (% w/w or Plato).
- AEcurrent beer - the current measured extract of the beer (% w/w or Plato)
- AEexpected final) - The expected final extract is taken from the fast ferment test (% w/w or Plato).
delta RE represents the weight percentage of residual fermentable sugar that is still present in the beer. From this it is easy to calculate the amount of carbonation that can be expected. Each % w/w (or Plato) of fermentable sugar will yield 0.5 % w/w CO2 and 0.5 % w/w alcohol. 1 g/l CO2 is also 0.1 % w/w CO2 which is used to calculate the expected carbonation from the real extract difference:
cresidual extract = 5 * delta RE
- cresidual extract - the carbonation from residual fermentable extract in g/l
Based on these calculations the following guidelines can be derived:
- Each degree Plato yields 4.1 g/l or 2 volumes CO2
- Each gravity point yields 1 g/l or 0.51 volumes CO<sub2</sub>
Final Remarks
While the number of formulas is daunting, they give the brewer more flexibility over the priming process especially since they can be combined. While priming with Kraeusen I may want to add sugar because the Kraeusen volume is to small or to far attenuated. Oftentimes I also have to account for remaining fermentable extract in the beer because I crashed the yeast to early or the fermentation was just dragging on. Because of that I created a spreadsheet (preloaded with US units|metric units) into which I simply enter all the data that I have and play with the volumes and amounts of sugar until the desired carbonation is reached.
sources
- [McGill] - Robert McGill, Priming With Sugar BYO article
- [ENSMINGER] - Peter A. Ensminger, Beer Data on HBD HBD article