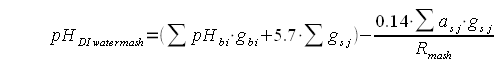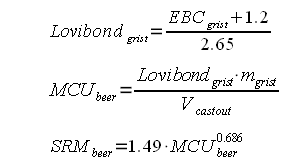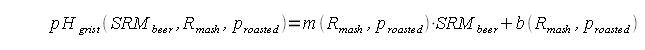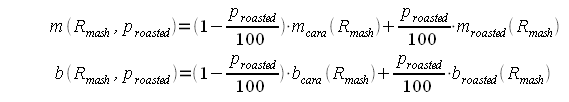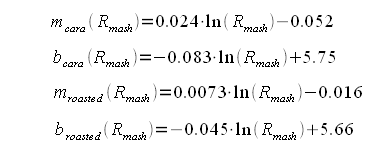Difference between revisions of "Beer color, alkalinity and mash pH"
| Line 71: | Line 71: | ||
As mentioned earlier the slope and y intercept of the linear function are determined by simple interpolation between the slope and y-intercept for "cara only" and "roasted only" recipes: | As mentioned earlier the slope and y intercept of the linear function are determined by simple interpolation between the slope and y-intercept for "cara only" and "roasted only" recipes: | ||
| − | + | [[Image:SRM_to_RA_slope_and_intercept.gif]] | |
| − | + | ||
Now for some more regression analysis. If the slopes and y-intercepts for "cara only" and "roasted only" recipes are plotted for the 4 different mash thicknesses (Figure 3) it is apperent that they can be fit with a logarithmic regression. The paramaters the were found led to the following formulas: | Now for some more regression analysis. If the slopes and y-intercepts for "cara only" and "roasted only" recipes are plotted for the 4 different mash thicknesses (Figure 3) it is apperent that they can be fit with a logarithmic regression. The paramaters the were found led to the following formulas: | ||
| − | + | [[Image:SRM_to_RA_parameters.gif]] | |
These formulas have been implemented in []. It should be noted that the approach outlined here only provides for a crude estimation of the mash pH and that there are cases where this prediction will not be correct. In particular when the distilled water mash pH of the base malts differ significantly from the pH values used in the simulation. Another limitation is the range of mash thicknesses. But it is assumed that the range of 2-5 l/kg should cover most practical mashes. | These formulas have been implemented in []. It should be noted that the approach outlined here only provides for a crude estimation of the mash pH and that there are cases where this prediction will not be correct. In particular when the distilled water mash pH of the base malts differ significantly from the pH values used in the simulation. Another limitation is the range of mash thicknesses. But it is assumed that the range of 2-5 l/kg should cover most practical mashes. | ||
Revision as of 13:37, 20 February 2010
|
This article uses results from mash pH experiments to shed light on the relationship between beer color, mash pH and water composition. It also develops a formula that can be used to make a crude prediction of the mash pH or the alkalinity necessary for a given mash pH based on the color and mash thickness of the beer. This formula has been implemented in the water calculator (Kaiser_water_calculator.xls) to predict the mash pH from beer color, mash thickness and water composition. Malt color, type and acidityBrewers know that darker malts are more acidic. But what does it mean for a malt to be more acidic? They for sure don't taste sour. Malt acidity is the ability to lower the mash pH and it can be measured via 2 means. One is the pH of a distilled water mash. Because of the absence of pH affecting ions the pH of that mash is determined only by the malt acidity and the mash thickness. Another approach is to take a sample from such a mash and add a strong base (e.g sodium hydroxide) to it until a predetermined pH (e.g pH 5.7) is reached. The amount of base added per unit of malt is a direct measure of that malts acidity. Testing the distilled water mash pH works well for base malts. Specialty malts, however, are generally much more acidic than base malts and testing their acidity through titration works better. In aforementioned mash pH experiments the following formula was developed for calculating the distilled water pH of a given grist. Where:
In English the weighted avarega of the distilled water mash pH for all the base malts and the titration point for specialty malts (5.7) is determined. This pH is then lowered by the acidity of the specialty malts. The more acidic they are, the higher their grist percentage and the thicker the mash is the more the lower the mash pH of the grist will be. Random recipe creation and pH and color calculationsAlong with the measured values for the distilled water pH of select base malts and acidity select select specialty malts 210 recipes were simulated. The recipes were thrown together randomly with the following constraints:
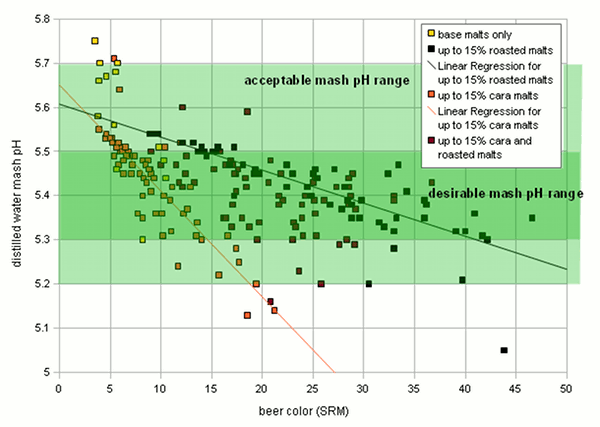
Crystal and roasted malts were treated as distinct groups since they also formed distinct clusters when their acidity was plotted over their color. For all these random recipes the distilled water mash pH of the grist and the color of the beer was calculated. The DI water mash pH was determined for 4 different mash thicknesses 2, 3, 4, and 5 l/kg. For the color calculation it was assumed that the total grist weighed 10 pound and the cast out volume was 5 gallon. The result were 4 sets of 210 data points that represent realistic combinations of beer color (SRM) and the distilled water mash pH of their grists. One set for every evaluated masch thickness (2, 3, 4 and 5 l/kg). The data for 3 l/kg is shown in Figure 1. Based on this chart we can make a few observations:
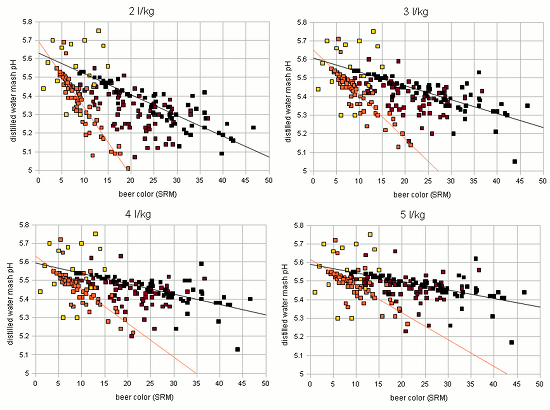
Figure 2 shows how the SRM to pH relationship changes for different water to grist ratios: the grouping remains the same, only the parameter for the linear functions change. With these observations the idea was born to estimate the grist pH from the color, mash thickness and the percentage of roasted malts in the specialty malt portion of the grist. I.e.if there are no specialty malts the linar function for "cara only" is used and if all specialty malts are roasted malts the linear function of "roasted only" is used. If there is a mix of the two a function that lies berween the two is used. Using the standard notation of a linear function the pH estimation from beer color and mash thicknes can be written as Where the new variable are:
As mentioned earlier the slope and y intercept of the linear function are determined by simple interpolation between the slope and y-intercept for "cara only" and "roasted only" recipes: Now for some more regression analysis. If the slopes and y-intercepts for "cara only" and "roasted only" recipes are plotted for the 4 different mash thicknesses (Figure 3) it is apperent that they can be fit with a logarithmic regression. The paramaters the were found led to the following formulas: These formulas have been implemented in []. It should be noted that the approach outlined here only provides for a crude estimation of the mash pH and that there are cases where this prediction will not be correct. In particular when the distilled water mash pH of the base malts differ significantly from the pH values used in the simulation. Another limitation is the range of mash thicknesses. But it is assumed that the range of 2-5 l/kg should cover most practical mashes.
|