Recently there has been a lot of focus on yeast growth calculators for starters. But most of the various calculators out there base their data on work published in Chris White and Jamil’s yeast book. Unfortunately the yeast growth example given in that book was only for a non agitated starter. When a starter is constantly stirred all the yeast is kept in suspension in a homogeneous nutrient environment. That is not true for non agitated starters where yeast will sediment and only evolution of CO2 will cause agitation. As a result stirred and still starters are expected to show different growth behavior that cannot be simply approximated by adding a constant scaling factor to yeast growth.
Jamil’s pitching rate calculator supports stirred starter fermentation but the growth curve used for that mode is a simple scaling of the growth curve for non agitated starters. Jamil never published how he arrived at the model used in his calculator. As a result I have to draw conclusions based on what I can observe when I run data points through his calculator.
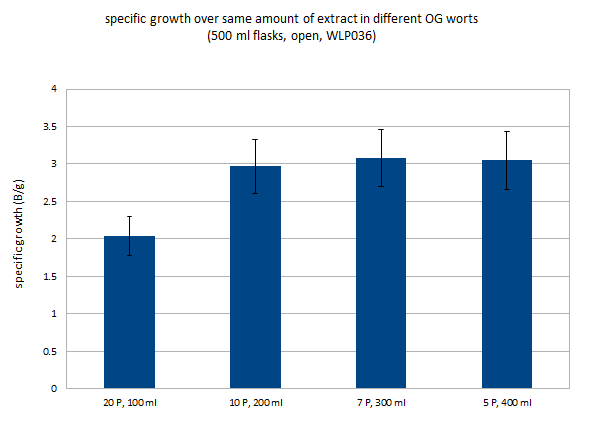
Before I get into comparing growth curves, I need to explain how I look at yeast growth. The primary factor in yeast growth is the available sugar. Within a practical range of wort concentrations the actual concentration of wort will have little impact on yeast growth. I’m still going to test this in a controlled experiment but observations from yeast propagation in my brewing seem to support that. Because of that I focus not not how many Million yeast cells are in a ml of wort, but rather how many Billion yeast cells get to share a gram of extract (sugars, proteins, minerals, etc) that is dissolved in that wort.
As for yeast growth, I care about how many new cells of yeast can be grown from that gram of extract. In their yeast book Chris and Jamil use a yield factor defined as new yeast growth in Million/ml per degree Plato drop of apparent extract. This takes into account that different worts can have different attenuation levels and with it varying amounts of fermentable sugars. While this is correct it requires knowledge of the wort’s fermentability and most brewers don’t know the fermentability of their starter wort. Furthermore the uncertainty of starter wort fermentability is likely +/- 5 % and this is well within the imprecision that one can expect from yeast calculators. I expect yeast growth calculators to have an error of +/- 15% or more. Because of that I feel confident in using Billion cells growth per gram of extract (B/g) as the yeast growth metric that should be tracked. Assuming a starter attenuation of 75%, the conversion factor between “yield factor” and specific growth (B/g) is 13.3:
1 B/g = 13.3 M/(ml*P)
Now that I established how I plot yeast growth I can show some charts.
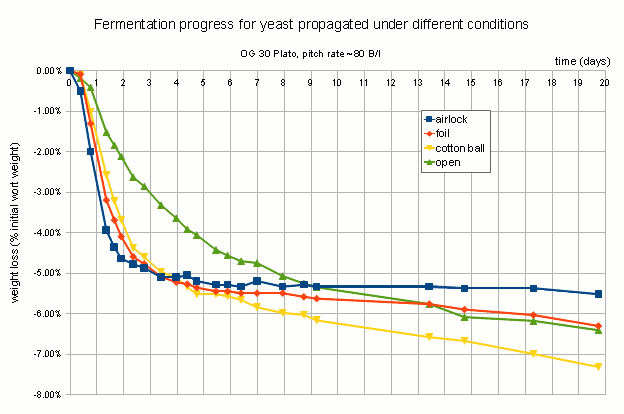
This one compared Mr Malty data for simple starters and stirred starters with the simple starter data from the Yeast book as well as a 2.7x scaled version of the simple starter data:
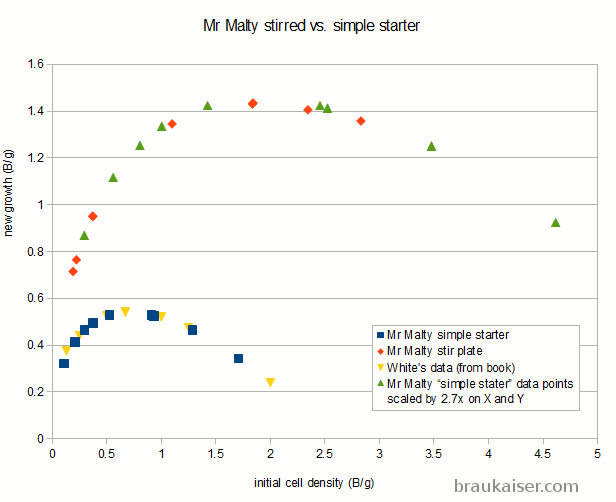
It is apparent that the growth curve for simple starter matches the data from the book, which makes sense. What surprises me, however, is that the stir plate data is not just scaling the yield for a given innoculation rate, but it also scales the inoculation rate. This means that the yeast growth calculator has different optimal innoculation rates for simple and stirred starters. That is something I don’t follow and my data contradicts that. More on that in a moment.
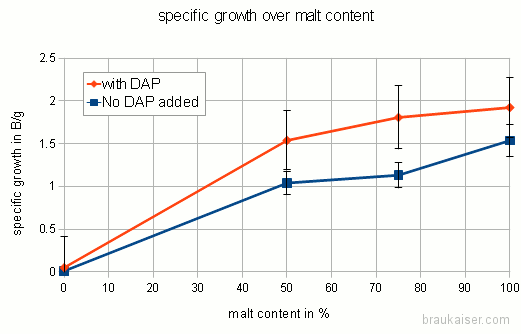
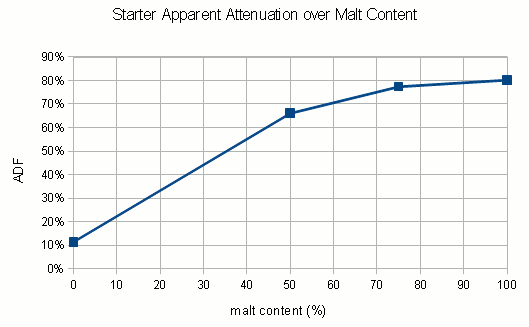
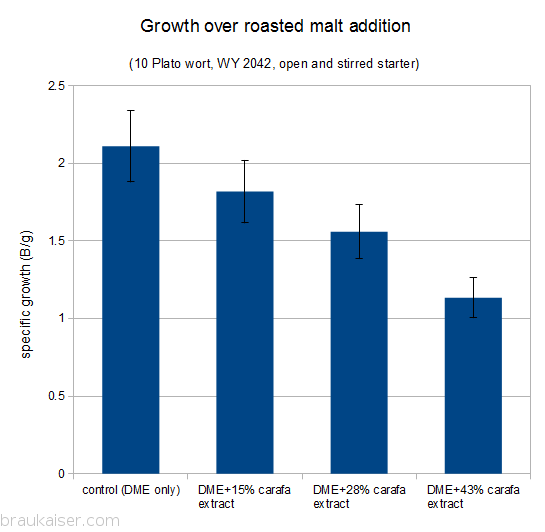
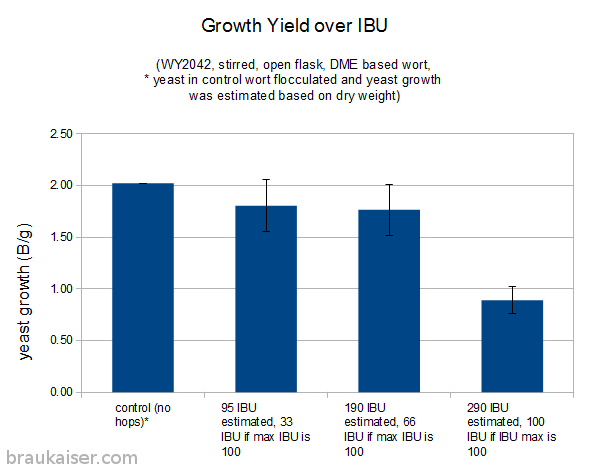
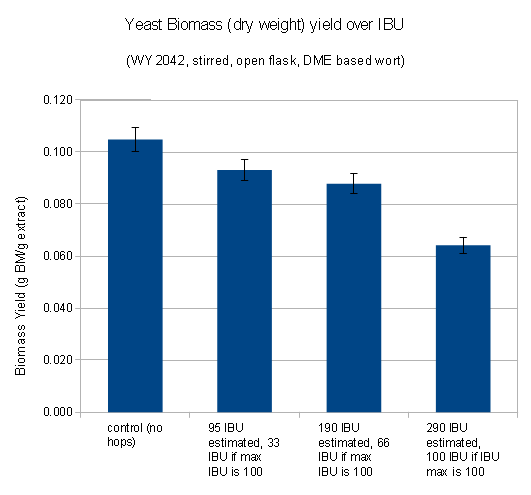
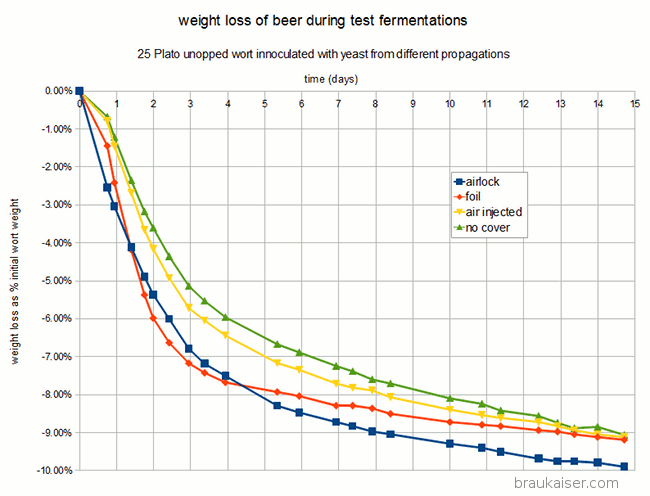
The following is a chart with my data. I have been using WY2042 since it is a low flocculant lager strain. Most of that has been presented in a previous blog post (Yeast growth experiments – some early results). What’s new is the non agitated data points and a few data points for using yeast that was stored in the fridge for 5 days before being used.
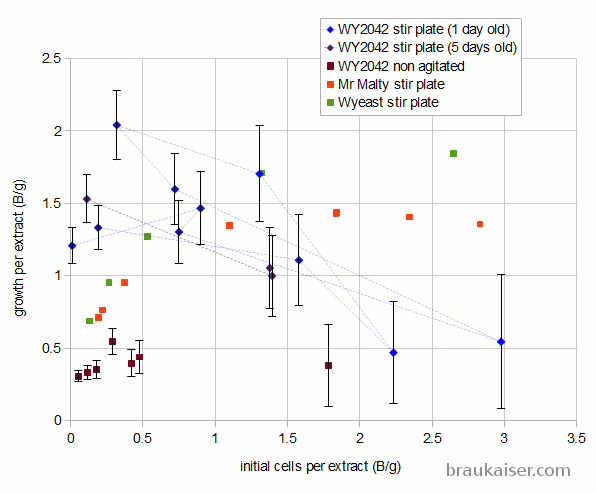 When the data is potted as growth in billion cells per gram over initial billion cells per gram, the data makes more sense. As the amount of extract available to each cell of the starting population approaches the amount of extract needed to grow a new cell, the growth per extract starts to fall. This is because the initial population is in a resting state and when sugar becomes available all vital yeast cells start to consume the sugar. A cell will not start budding unless it consumed all the resources needed to grow a new cell. If this was an ideal culture, where every cell consumes sugar at the same rate and needs the same amount of sugar to grow a daughter cell, cell growth would stop once there are more cells per gram of extract that it takes to grow the same amount of cells. This is because none of the cells would have access to the amount of nutrients needed to grow a new cell. But this is not such an ideal culture and some cells will consume nutrients faster than others and will be able to grow daughters while others can’t.
When the data is potted as growth in billion cells per gram over initial billion cells per gram, the data makes more sense. As the amount of extract available to each cell of the starting population approaches the amount of extract needed to grow a new cell, the growth per extract starts to fall. This is because the initial population is in a resting state and when sugar becomes available all vital yeast cells start to consume the sugar. A cell will not start budding unless it consumed all the resources needed to grow a new cell. If this was an ideal culture, where every cell consumes sugar at the same rate and needs the same amount of sugar to grow a daughter cell, cell growth would stop once there are more cells per gram of extract that it takes to grow the same amount of cells. This is because none of the cells would have access to the amount of nutrients needed to grow a new cell. But this is not such an ideal culture and some cells will consume nutrients faster than others and will be able to grow daughters while others can’t.
I also expect that yeast growth of a large population of older cells is reduced compared to young cells since the old cells will need to fill their reserves before they can start accumulating nutrients for growth. I don’t have enough data on that yet to quantify this effect.
This effect of dropping yeast yield is not as pronounced for a non agitated culture. This is because in such a culture not all yeast cells have the same access to wort nutrients due to sedimentation. Yet another reason why one cannot estimate the yeast growth characteristics in a stirred starter from a non agitated starter.
Based on my observations and knowledge of yeast growth so far, I think the following yeast growth model should be used for calculating expected yeast growth in stirred starters:
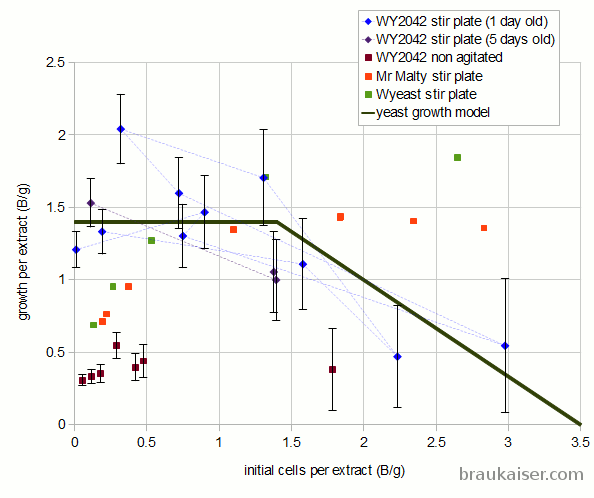
If (initial cells < 1.4 Billion/gram extract)
yeast growth is 1.4 Billion / gram extract
If (initial cells between 1.4 and 3.5 Billion / gram extract)
yeast growth is 2.33 - 0.67 * Billion initial cells per gram extract
else
no yeast growth
For non agitated starters a growth rate of 0.4 Billion per gram should be assumed over the full initial cell density range (0 – 3.5 B/g). I don’t think that starters with more than 3.5 Billion cells/g are practical. I expect the growth rate in starters to be affected by the shape of the vessel, the volume of the wort and more. The 0.4 Billion new cells per gram proposed here is a rough guess based on the data points I have so far.
Update:
The proposed model for stirred starters has been implemented in: